LA HISTORIA DE LA ECUACIÓN POLINÓMICA DE TERCER GRADO.
Nuestra historia se sitúa en el siglo XVI y tiene como protagonistas principales a Niccolo Fontana, Girolamo Cardano, Scipione del Ferro y Ludovico Ferrari y como actores secundarios a Antonio Maria del Fiore y Annibale della Nave.
Sobre la década de los 30 de este siglo, llega a oídos de Tartaglia que un tal del Fiore posee un método para resolver ecuaciones cúbicas. En una época como aquella, en la que el interés por el álgebra estaba creciendo de manera significativa entre los matemáticos en Europa, poseer un método para resolver estas ecuaciones resultaba valiosísimo. Por ello, Tartaglia se puso a trabajar en el tema, encontrando tal método por sí mismo un tiempo después.
En aquella época, era habitual organizar desafíos entre matemáticos en los que cada uno proponía problemas que el otro tenía que resolver. Pues a raíz del trabajo de Tartaglia, se organizó uno que lo enfrentaba a del Fiore, resultando Tartaglia ganador de manera aplastante (resolvió todos los problemas propuestos por del Fiore, mientras que este no fue capaz de resolver ninguno de los que le tocaron).
Cuando Cardano tuvo conocimiento de esta aplastante victoria de Tartaglia, intenta convencerlo para que le revele el método que había descubierto y así poder publicarlo en su obra Ars Magna, que estaba preparando en aquellos años. Aunque Tartaglia se niega en primera instancia, al final le revela su descubrimiento con la condición de que no lo publique (aunque, al parecer, Cardano estaba dispuesto a otorgarle a Tartaglia en su obra la autoría del descubrimiento).
Lo que Tartaglia había descubierto eran métodos para resolver las ecuaciones cúbicas que no tienen término de grado dos. Aunque en la actualidad todas ellas se reducen a una única forma, en aquella época se expresaban de estas tres maneras, x3+px=q, x3=px+q y x3+q=px, y cada una tenía su propio método de resolución (los números negativos todavía no se aceptaban con demasiada naturalidad). A partir de estos métodos, Cardano y su ayudante Ludovico Ferrari consiguen un método para resolver la cúbica general x3+mx2+nx=r. Esta ecuación puede reducirse fácilmente a una del tipo x3+px=q, por lo que solamente haría falta resolver ésta. Sus soluciones vienen dadas por la siguiente expresión:
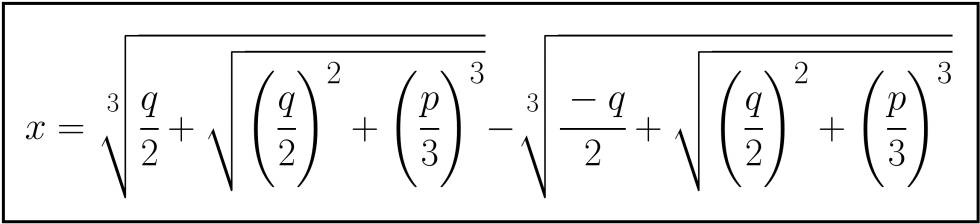Aunque parece que solamente tenemos un valor, en realidad esta expresión representa los tres valores de las tres soluciones de la cúbica general. Dos de las soluciones contenían raíces cuadradas de números negativos, dando lugar a lo que hoy conocemos como números complejos. Y aquí viene la clave de la historia: del Fiore conocía el método de resolución porque Scipione del Ferro, profesor suyo, se lo había comunicado años antes. Es decir, del Ferro fue el primero que creó un método de resolución para una cúbica. En 1542, Cardano y Ferrari viajan a Bolonia en busca de los trabajos de del Ferro, y es Della Nave (yerno de del Ferro) quien se los proporciona. Al verlos, Cardano comprueba que el método de del Ferro para resolver la cúbica x3+px=q era el mismo que el de Tartaglia, por lo que entiende que la promesa que le había hecho este de no publicar su descubrimiento ya no tiene validez. Cardano publica el método de del Ferro en Ars Magna en 1545, y Tartaglia entra en cólera. Aunque Cardano lo nombra varias veces en su obra, Tartaglia se siente traicionado y responde publicando un año después un libro con su método y con ataques a Cardano. Este no responde a dichos ataques, pero sí lo hace Ferrari. Este enfrentamiento acaba con un nuevo “duelo matemático” entre Tartaglia y Ferrari que se convierte en un auténtico fenómeno social. Durante el duelo se produce una discusión por uno de los problemas, lo que lleva a aplazarlo al día siguiente. Pero Tartaglia, al parecer por el apoyo de la multitud a Ferrari, no se presenta, por lo que Ludovico es declarado ganador.
